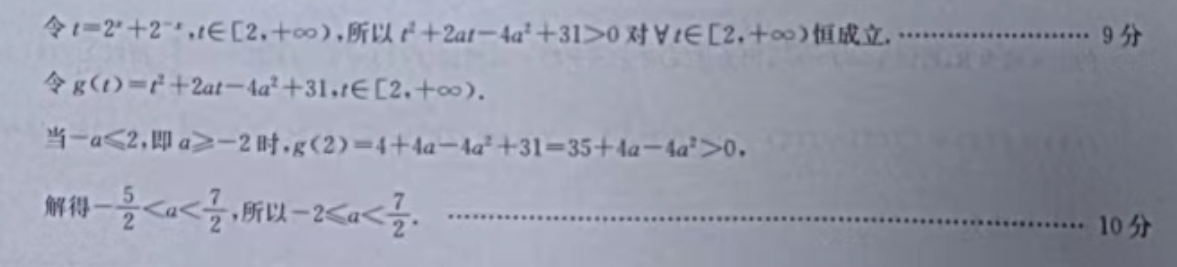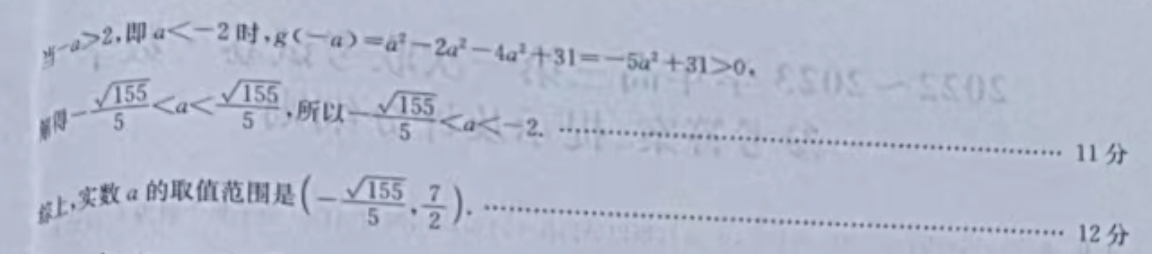2022-2023九年级上册英语学生双语报答案，目前学生双语报答案网已经整理了2022-2023九年级上册英语学生双语报答案的各科答案和试卷，更多学生双语报答案请关注本网站。

2.0fCr）=-e-2ar=-x(e+2a）.1分10时，令了C)>0,解得r<01令了(x)<0,解得x>0,所以了x)的单调递减区间为(0.+o).)的单调递增区间为（一0∞，0)：…2分h(-2a)=0.即a=一专时，了()≤0在(-0，十∞)上框成立，所以了(x)的单调递诚区间为(-00,十0)……3分5h(-2a)<0,即-2 0,解得lh(-2a)<<0,令了(x)<0,解得r<1n(-2a或>0，所以f(r)的单调递增区间为(n(一2a),0),f(x)的单调递减区间为(-，ln(-2a),(0,十∞)…4分当n(-2a)>0,即a<-2时，令了(x)>0,解得0 h(-2a),所以f(x)的单调递增区间为(0，ln(-2a)),了(x)的单调递减区间为(-∞，0)，(h(-2a）,十0∞)。…5分2证明：令1x)=0,即1-x)c-a(2+1D=0,即9-4，所以9-产x+1十1)=,所以g(n)=g(),所以g)=T3C,令g>0,解得r<0,(x+1)令g(x)<0,解得x>0,所以g(x)在（一∞，0）上单调递增，在(0，+∞)上单调递减，又当x<1时，8(x)>0,当x>1时，g(x)<0,不妨设<，则)<0<<1.……8分要证1十x1<0,即证五 <一1，又g(x)在（一∞，0）上单调递增，所以只需证g(1)

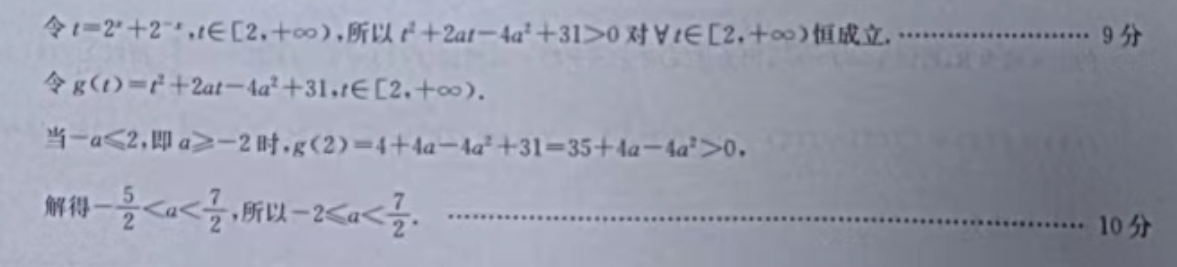
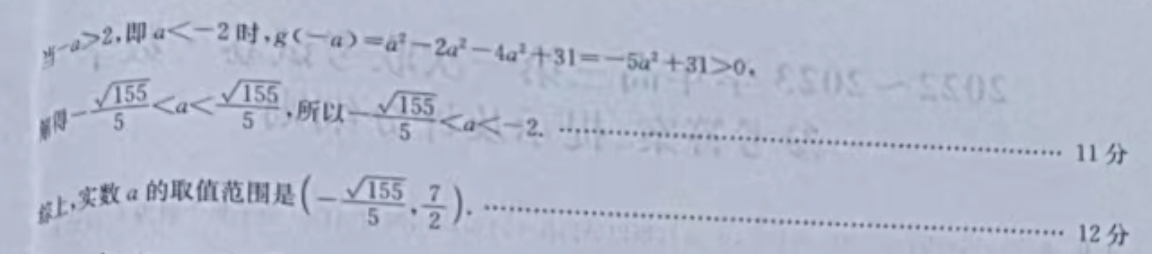
2孔.1解，因为/C)是定义在R上的奇函数，所以0)-老-0，解得6=-3，…1分1+a所以f(x)=31-33'+a又)是定义在R上的奇函数所以-1少-10).。-。，解得a-。…2分当a=16-3时，1)-等+所以-)--罗-1，符合题意所以a=1,b=-3.…3分(2)f(x)在（一oo,+o∞）上单调递增，4分证明：设n<,所以f）-f)-30-3-311=36(3h-34)39+139+1(3别+1)(39+1，…6分又n 0,39+1>0，所以f(n)-f(n)<0,即f() 0,得了(4+a·2+1)>-(+a·2+1+33-4a2),又f(x)是定义在R上的奇函数，所以f(4+a·2+1)>f(-4“-a·2+1-33+4a2).又了(x)在(-e0,+c∞)上单调递增，所以4"+a·21>-4-a·2+1-33+4a2,所以4"+4+a·(21+21)-4a+33>0.令1=2+2‘，t∈[2，十co),所以2+2a1-4a2+31>0对y1∈[2，+o∞)恒成立.…9分令g(t)=2+2at-4a2+31,1∈[2，+o∞).当-a≤2，即a≥-2时，g(2)=4+4a-4a2+31=35+4a-4a2>0,解得-是 2.即-2时.80-820-0t31=对+>，505505,所以停<211分,实数：的取值花围是(-西)12分