2022-2023高二学生双语报33期b4答案，目前学生双语报答案网已经整理了2022-2023高二学生双语报33期b4答案的各科答案和试卷，更多学生双语报答案请关注本网站。

解：(1)AB=(2-k,-k-t,3-t),CD=(2,0,-4),因为AB∥CD,所以存在唯一实数入，使得AB=入CD,所以(2-k,一k一t,3一t)=(2λ，0，-4入)，2-k=2λ，A=-52’所以{一k一t=0,解得k=7,3-t=-4入，t=-7,所以k=7,t=一7.(2)BC=(-2,1,0),则cos(BC,CD)=BC.CD-42Bc11CD5×25设直线BC与CD所成的角为0，4√2I25=5所以，点B到直线CD的距离为BCIsin0=5X②T-√1055

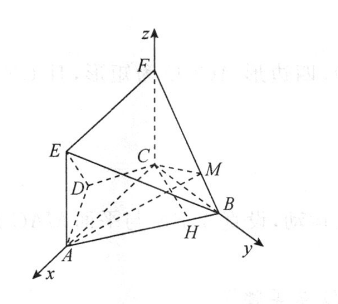
(1)证明：由已知可得四边形ABCD是等腰梯形，过C作CH⊥AB,垂足为H,则BH=2=1221在R△BCH中，CH=VBC-册-，-52则sin∠CBH=12,可得∠CBH=60.在△ABC中，由余弦定理可得，AC=AB+BC2-2AB·BC·cos∠CBH=4+1-2X2X1X号-3，则AC2十BC2=AB2,所以AC⊥BC.又CF⊥平面ABCD,ACC平面ABCD,所以CF⊥AC,因为BC∩CF=C,BC,CFC平面BCF,所以AC⊥平面BCF.又四边形ACFE为矩形，所以AC∥EF,则EF⊥平面BCF,而BCC平面BCF,而BCC平面BCF,所以EF⊥BC.(2)解：因为CF⊥平面ABCD,且AC⊥BC,以C为坐标原点，分别以CA,CB,CF所在直线为x,y,之轴建立如图所示的空间直角坐标系，则A(5,0,0),B(0,1,0),F(0,0,1),E(3,0,1),因为M∈BF,所以设M(0,1-a,a),0