2022-2023学生双语报exo答案，目前学生双语报答案网已经整理了2022-2023学生双语报exo答案的各科答案和试卷，更多学生双语报答案请关注本网站。

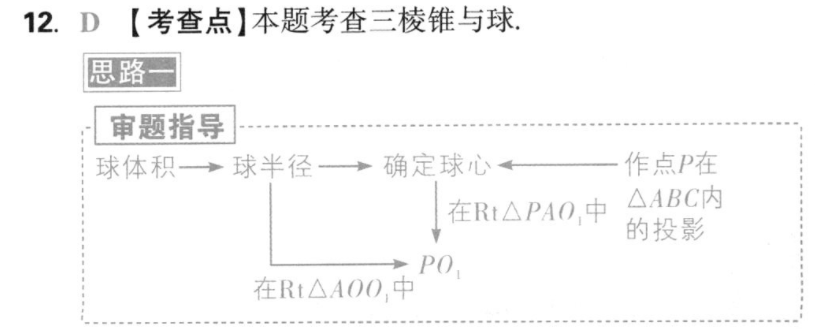
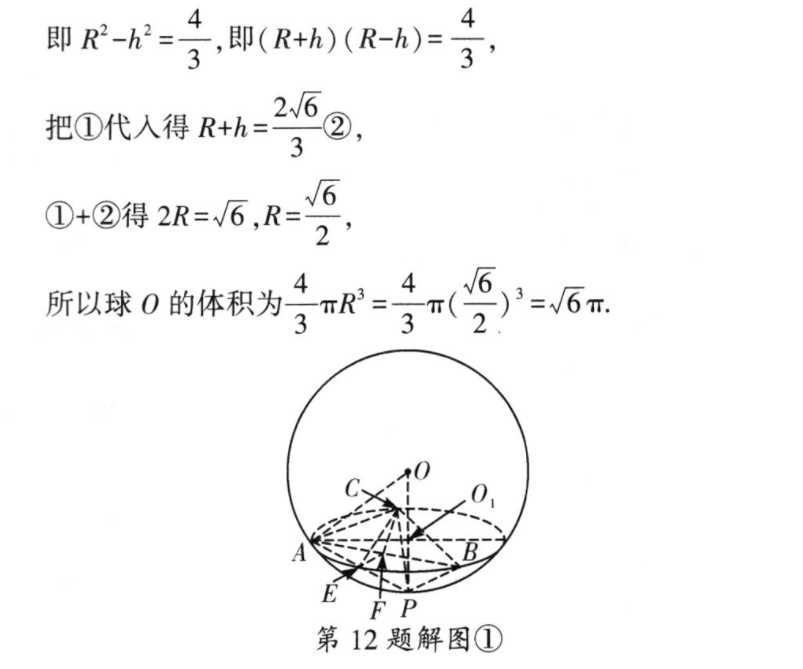
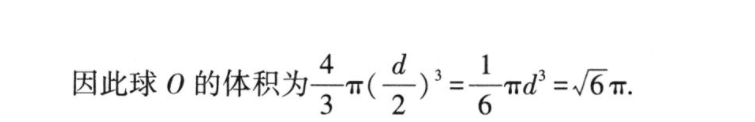
12.D【考查点】本题考查三棱锥与球思路审题指导球体积→球半径→确定球心《作点P在在Rt△PAO,中△ABC内的投影PO在Rt△AOO,中【解析】设O,为P在△ABC内的投影如图①所示设PA=PB=PC=a,球0半径为R,O01为h.在△PAC中有PA=PC=a,AC=2,E为PA中点，PA2+AC2-PC2cos∠PAC=2PA·ACa2+4-a21Aaa从而CE=√AC2+AE2-2AC·AEcos∠PAC=2+又∠CEF=90°，得CE2+EF2=CF2,即2+年+（分）2=3，则a2=2,在R△P0A中，由P=P0+A0得2=P0+(后2，又0，=0，即R-h=,√634在Rt△A00,中，由0A=A0+00号得R=+h,即R-2=号，即(R+h)(R-h)=44把①代入得R+h=262,①+②得2R=6,R=,所以球0的体积为号n=号（气=，6n4F P第12题解图①思路审题指导P-ABC中，PA=PB=PC、垂直关系、补形为△ABC为正三角形正三棱锥性质正方体球体积确定外接球直径【解析】如图②，由PA=PB=PC,△ABC是边长为2的正三角形，可知三棱锥P-ABC为正三棱锥则顶点P在底面的射影为底面三角形的中心，连接BO并延长交AC于G,F则AC⊥BG,又PO⊥AC,P0O∩BG第12题解图②=0,可得AC⊥平面PBG,则PB⊥AC,又∠CEF=90°，则CE⊥EF,因为E,F分别是PA,AB的中点，所以EF∥PB,于是PB⊥CE.又CE∩AC=C,因此PB⊥平面PAC,即PB⊥AP,PB⊥CP,所以三棱锥P-ABC的三条侧棱两两互相垂直，所以三棱锥P-ABC的外接平行六面体为棱长为2的正方体[点拨]根据垂直关系将三棱锥补形为易于求外接球体积的正方体进行求解其外接球的直径d为该正方体的体对角线，长为√6，因此球0的体积为号（号）=d=6m

【答案】ABC【解折】fx)=in-sn(aur+写）=sin-sin c行-coin了=2 sin-π132 cos wz=sin(wx-）,周为x∈[0，，所以r-首-台o-引又画数fx)在区间[0，上的值线为[-，小0)=所以由正孩函数的对春性，只高智≤@一音≤行得骨< <号，因此ab,c率可能取得，d不可能取得。52< p>