2022-2023学生双语报x54版答案，目前学生双语报答案网已经整理了2022-2023学生双语报x54版答案的各科答案和试卷，更多学生双语报答案请关注本网站。

曲线-是=1(>0，b>0)的左、右焦点分别为F1,F:,过F,且斜率为一37的直线与双曲线在线限的交点为A.若(F1F。+F1A)·F2A=0,则此双曲线的渐近线方程为【源验Ay=士xB.y=士√Ex的s=。Cy=土7xD.y=士3x1话【答案】D【解析】由题意可知，F2A-F1A-F1F2,若(F1F,+F1A)·F2A=0,即(F1F2+F1A)·(F1A-F1F2)=0,可得F1A=F1F22,即|AF11=|F1F2=2c.由双曲线的定义可知|AF2|-|AF1I=2a,可得AF21=2a+2c,因为过F,的直线斜率为-37，所以在等腰三角形AF,F,中，an∠AFF,=-37,则cos∠AF,F:=-日，由余度定豆得0B∠AFR,-如+2g-日化满得：=2a中。-6-可香名-5所以此风2·2c·2c曲线的渐近线方程为y=士√3x,

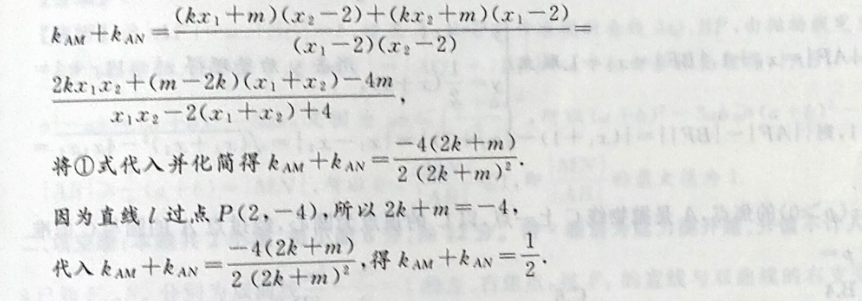
12.(20分)已知椭圆E:若+芳=1a>6>0)的离心率为，且过点1，号,其下顶点为A若斜率存在的直线1交椭圆E于P,Q两点，且不过点A,直线AP,AQ分别与x轴交于点M,N.(1)求椭圆E的方程；(2)当M,N的横坐标的乘积是时，试探究直线1是否过定点，若过定点，求出定点坐标；若不过，请说明理由。3解：(1)由离心率e=_3aa①，将1，)代入稀国E的方程得34b31②，由①②得a2=4,b2=1,两斯：放两4，人千圆景交证，A材验直滑健食M点丝：点衡1喻所以描围E的方粒为写+)=1。,点宝出果并，点安长人处直：量(2)由(1)知：A(0,-1).一华一有的围路热，8平心份光的设直线l的方程为y=kx十m(m≠-1)，P(x1,y1),Q(x2,y2),9则直线AP的方程为y=+z-1,令y=0,得点M的横坐标为xw=y1+1同理可得点N的横坐标为xN=y2+11所以xMxN=x1X2反牙水看正桥：A济不手特的8A典直等①，(，0)认峡(y1+1)(y2+1),x172(kx1+m+1)(kx2+m+1)x1x22x1x2十k(m十1)(x1十x2)十(m十1)2：m意要角，m+=元长珠长08人数，善A华y=kx+m,4+y2=1,由得(4k2+1)x2+8kmx+4m2-4=0,则△=642m2-4(4k2+1)(4m2-4)>0,解得m2<4k2+1,8km4m2-4所以x1+x:=一46+1x:=4k2+14m2-44k2+1所以wvg,+k0m+D-(司+m+23,又m≠一1，4k2+1可化海得解得a-2。所以l:y=kx十2，所以直线1过定点(0,2).已知椭圆C,十61(>b>0)的左焦点为F,离心率为二，过点F且垂直于x轴的直线被椭圆C截得段长为2.(1)求椭圆C的方程：(2)已知点A(2,0),过P(2,-)的直线1交椭圆C于M,N两点，证明：直线AM的斜率与直线AN的斜率之和为定值。衣路张林海物华的【的嫩(1)解：设椭圆C的半焦距为c,则2b2=2,弹，亲通aa2=b2+c2,a=2,解得b=√2所以精国C的方粗为号+号-1任【资被(2)证明：由题意知直线l的斛率存在，设其方程为y=kz十m(k≠0)，M(x1y),N(xy),、验独限y=kx+m,联立方程组消去y并整理得(2k十1)x2十4kmx+2m2-4=0,△=(4km)2-4×(2k2+1)(2m2-4)=32k2-8m2+16>0,4km则1+x,=一2k+7x1x:2m2-42k2+1①8又大AM十kAN=y2)【海1x1-2x2-2将y=kx1十m,y2=kx2十m代入，整理得饰粉年，(，生)，又)能保科原的其高，人数得衡kw+kw=k1十m)(:-2）+(k.x,十m)(x1一2)(x1-2)(x2-2)2kx1x2+(m-2k)(x1+x2)-4mx1x2-2(x1+x2)+4-4(2k+m)将①式代入并化简得kAw十kAN=2(2R+m)因为直线1过点P(2,一4)，所以2k十m=一4，代入w+心-224得w十心1