2022-2023学生双语报31期高三答案，目前学生双语报答案网已经整理了2022-2023学生双语报31期高三答案的各科答案和试卷，更多学生双语报答案请关注本网站。

9若双自线后y2=1(a>0)的离心率为2，则其渐近线方程为【答案】y=土√3x=2,解得Q=2,因此该双曲线的渐近线方程为y=士。t±√5x,

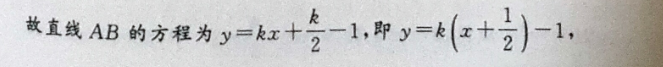
11.(20分)已知椭圆C是+是=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系，直线l:x-一y+厄=0与以原点为圆心，以椭圆C的短半轴长为半径的圆相切.(1)求椭圆C的方程；(2)设M是椭圆C的上顶点，过点M分别作直线MA,MB交椭圆于A,B两点，设两直线的斜率分别为k1,k?,且k1十k2=4,证明：直线AB过定点，并求出该定点.(1)解：因为等轴双曲线的离心率为√2，所以椭圆C的离心率e=2(1,0)A:(1出)所以e2-c=a二b=a22,所以a2=26.（0,n)0:(6,1,1=m)0+来0直因为直线x一y十2=0与圆x2十y2=62相切，0M点精，0-◆，-=气收脉的人逸直国所以b=1,所以a2=2,所以箱国C的方程为号十y=1%低济绕秘钟人名，朝章题同(2)证明：由(1)可知M(0,1),①若直线AB的斜率不存在，设其方程为x=x0,则A(xoyo),B(x0,一yo).由已知得0一1+一01-4，解得xo=-xo211第1所以此时直线AB的方程为x=一(中路个A)于十+王231②若直线AB的斜率存在，设AB的方程为y=kx十m,依题意m≠士1.m)++3十)y=kx十m,度设A(x1,y1),B(x2,y2),由0十x8+x(1)得(1+2k2)x2+4kmx+2m2-2=0,△>0.4km2m2-21+2k2x1x2=1+2k2由1十2=4，可得一1+y,-1片以起十m-1:十m=1-4,即2k+(m-1号=4持十江，代入得人一-2ZIZ2o)x1工2所以k=2(m十1)，所以m=一1k故直线AB的方程为y=红+合一1，即)=（十号）一1，所以直线AB过定（一合，一小综上，直线AB过定点(-2，-