2022-2023学生双语报w版高一30答案，目前学生双语报答案网已经整理了2022-2023学生双语报w版高一30答案的各科答案和试卷，更多学生双语报答案请关注本网站。

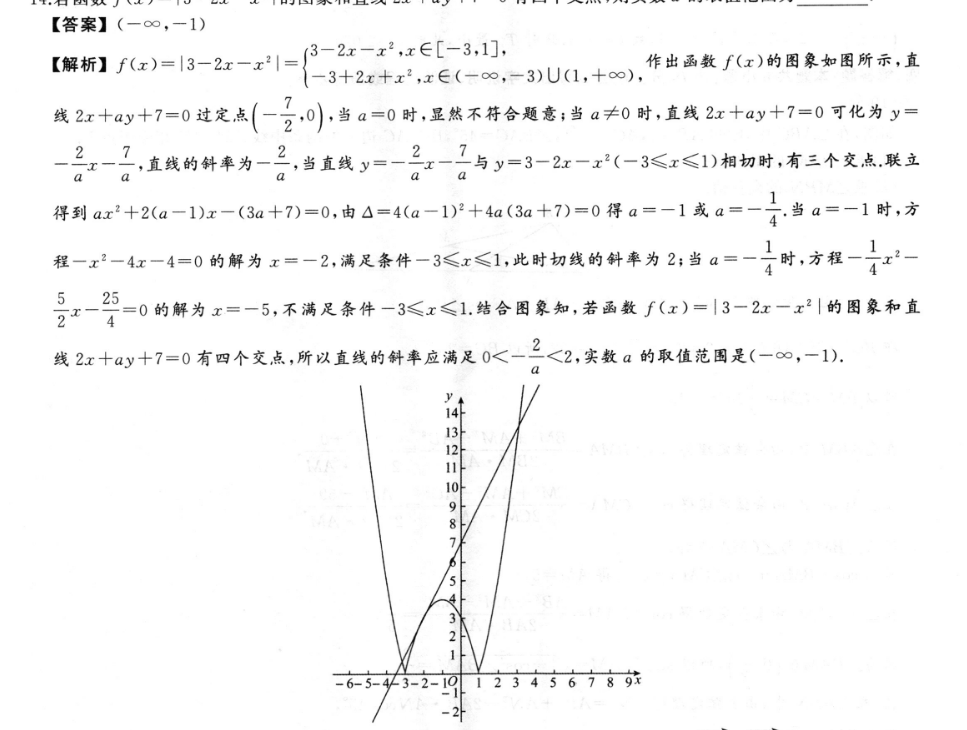
【答案】(-∞，-1)【g1e)-13-2-r=22iUa+作出函数f(x)的图象如图所示，直线2z十ay+7=0过定点(-20），当a=0时，显然不符合题意：当a≠0时，直线2红十ay+7=0可化为y=-?,直线的斜率为-2，当直线y=-二x-7与y=3-2红-(-3≤x≤1相物时，有三个交点联立a得到ax+2a-1r-(3a+)=0,由4=4a-12+4a(3a+7)=0得a=-1或a=-子当a=-1时，方程-x-4红-4=0的解为x=-2,满足条件-3

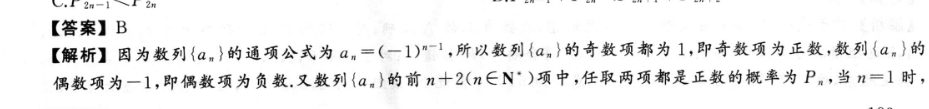
2n112n【答案】B【解析】因为数列{am}的通项公式为am=(一1)n1,所以数列{am}的奇数项都为1，即奇数项为正数，数列{am}的偶数项为一1，即偶数项为负数.又数列{am}的前n十2(n∈N·)项中，任取两项都是正数的概率为P。,当n=1时，3项中，任取两项都是正数，概率为P,=3,故A错误；将2m-1代入，数列{a,}的前2m十1(m∈N)有(n+1)个正数，n个负数，任取两项都是正数的概率为P2m-1Ch+=n(n+1)n+1C+1(2n+1)·(2n)=4n+2,将2n代入，数列{am}的前2n十2(n∈N·)项中，有(n十1)个正数，(n十1)个负数，任取两项都是正数的概率为P2m=C+1=C+2n(n+1)（2m+1)20十2)=4n十2，将2m十1代入，数列{a,}的前2m+3(n∈N)项中，有(m十2)个正数，(m十1)个负数，任取两项都是正数的概率为P2m+1=Cg+2=（n+1)(n+2)C=27+3)2n2)=十6，将2m+2代入，数列1a.}的前2m+4(n∈N)项中，有(n+2)个正数，(n十2)个负数，任取两项都是正数的概率为P+?=Ca+2=C2m+4(n+1)(n+2)n+1nn十1-2(2n+3)(2n+④=4n+6,所以P.-P+:=4n+2一4n+6=4n+2)4m+6<0,所以P. 0，所以P-1>Pm,故C错误；(P-1十Pn)-(P2+1十P+2)=n十2n十114n+24n+622错误.,4【答案】D【解析】因为f(x)是定义在R上的奇函数，所以f(0)=0,当x∈[0,1]时，f(x)=a十b,f(1)十f(0)=f(1)=3,则士h=0解得a=4{a+b=3,行{b=-1,所以当x∈[0,1]时，f(x)=4一1，因为f(x)是奇函数，所以图象关于原点对称，又f(2一x)=f(x),所以f(x)的图象关于直线x=1对称，由此画出f(x)在区间[一2,5]上的图象如图所示，由图象可知方程f(x)=一1有4个解，也即g(x)=f(x)十1=0有4个解，即g(x)在区间[一1,5]上有4个零点.P=2y=-1