2022-2023学生双语报七下40期答案，目前学生双语报答案网已经整理了2022-2023学生双语报七下40期答案的各科答案和试卷，更多学生双语报答案请关注本网站。

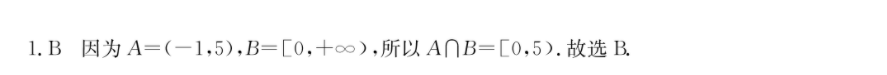
1.B因为A=(一1,5)，B=[0,十∞)，所以A∩B=[0,5).故选B.

8.A法一：e1-mx-2n-3≥0即e-1-3≥mx十2m,令f(x)=e1-3,g(x)=m.x+2n,则f(x)≥g(x)恒成立，即曲线y=e-1一3在(.xo,eo-1一3)处的切线方程为g(x)=m.x十2m时，f(x)≥g(x)恒成立.因为f(xo)=eo-1,其切线方m=ero1,程为y=eo-1x十eo-1一3一xoeo-1,所以2n=eo-1-3-xoe0-11且m>0,得2m=-3-mlnm,所以”=-32m,令hm)=一b”,所以(m)=品一，从而Am》在0.3)止单递增，在3，十o∞)上单调递减，2m则品的最大值为么(3)=-b故选A法二：设f(x)=e1一m.x-2n-3,则f(x)=e-1-m,当m<0时，f(x)>0,则f(x)在R上为增函数，此时f(x)在R上没有最小值，且当x→一∞时，f(x)→一∞，此时不合题意；当m>0时，f(x)<0台x<1十ln;f(x)>0台x>1十lnm,所以f(x)在（一o,1+lnm)上为减函数，在(1十lnm,+o∞）上为增函数，从而f(x)mm=f(1+lnm)=一mlnm一213.若f)20恒成立，只需f)m=一mlm2m-3≥0，解得2m≤-mlnm-3,于是开≤一mm-3.令g()=2m-是（血m+品）水m>0.则g(m)=一n3,可得gm）m=g3)=-,所以品的最大值为-b放选A