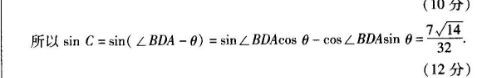
18.【试題情境】本题是基础性题目,属于课程学习情境,具体是数学运算学习情境,以平面图形为载体考查余弦定理与三角恒等变换【关键能力】本题考查逻辑思维能力和运算求解能力余弦定理【解题思路】(1)在△ABD中,AB=6,cB=4,AD=4∠ADB为锐角BD=5或BD=4→BD=5余弦定理在△ABC中,AB=6,csB=4,AC=6∠BAD=2DAC弦定理(2)记∠DAC=6∠BAD=2三角恒等变换同角三角函数的基本关系式16, sin 6=两角和的正、余弦公式7,m3=8sinC=sin(丌B-36)=sin(B+36)=解:(1)在△ABD中,由余弦定理得cB=2AB,BD,所以4=2X6XBD,解得BD=5或BD=4(2分当BD=4时,ADB=1+636<0,则∠ADB>,不合题意,舍去(3分)当BD=5时,c0∠ADB=15+3536>0,则∠ADB<,符合题意故BD=5.2AB·BC,所以3=36+在△ABC中,B=AB+BC-A2×6×BC得BC=12,所以DC=7(6分)(2)解法一记∠DAC=8,则∠BAD=29在△ABD中,cos∠BAD=cos26=所以6为角012:m2,02分)所以sin=COs 0=(8分)所以sin36=sin20osb+cos26sin6=同理cos36=(10分)易得smB=EfLA sin C= sin(T-B-30)=sin(B+30)=sin Bcos 38+cos Bsin 38(12分)解法二记∠DAC=日,则∠BAD=26在△ABD中,cos∠BAD=cos2e、AB2+AD-BD292AB·AD所以为锐角,n2e=1-cos2所以sin=∠BDA=AD2+BD2-AB216+25-36DAAD·BD2×4×5-8,8in∠BL(10分)所以sinC=sn(∠BDA-6)=sin∠ BDAcos 6-cos∠ BASin=7√143212分

11.ACD【关键能力】本题考查逻樨思维能力、运算求解能力【学科素养】试题借助与拋物线相关的命题的判断,考查考生对抛物线的性质的掌握情况以及利用解析几何的想方法解决问题的能力,体现的学科素养是理性思维、数学探索【解题思路】设A(4,),B(4,n),直线AB的方程为x=+1,将直线AB的方程代入抛物线方程,利用根与系数的关系得y1y2=-4对于选项AB,利用向量知识研究AC与BC、AC与MF的位置关系即可;对于选项C,可利用抛物线的定义确定AF,BF的长度,然后判断等号是否成立;对于选项D,利用导数的几何意义确定以点A为切点的切线方程,然后验证点C的坐标是否满足切线方程即可.【解析】如图,由题意可得F(1,0),准线方程为x=-1.设A(,y1),B(,y2),直线AB的方程为x=y+1,代人抛物线方程得y2-4-4=0,所以yy2=-4.因为线段MN的中点为C,所以C(-1,12),所以=(+1,xy),C=2+2,所以d=倍1+22=0,所以AC⊥BC,故A正确因为M(-1,y1),所以M=(2,-y1),所LCA. MF2+20,所以AC⊥MF,所以四边形AMCF的面积等于方|AC|IMF,故B错误根据抛物线的定义知|AFI=lAM=2+1,BF-1BN=2+1,所以1AF+BF=x+x+,AF1,BFl6++A+1+2+2,所以|AF|+1BF|=HAF·1BF|,所以C正确不妨设点A(,y)在x轴上方,当y>0时,由y2=4x得y=2,y=,所以抛物线以点A为切点的切线方程为)+y1=-x+,令x=-1,得12=+,所以点C在以点A为切点的切线上,即直线CA与抛物线相切,故D正确.故选ACD.

以上就是英语周报八年级下册新目标第20期2018－2022答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/21721.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。