23.【命题意图】本题考查绝对值不等式的求解,考查推理能力与计算能力【解析】(1)依题意,1x+21-21x-11+3<0,当x<-2时,-x-2+2x-2+3<0,解得x<1,故x<-2,(2分)当-2≤x≤1时,x+2+2x-2+3<0,解得x<-1,故-2≤x<-1,…(3分)当x>1时,x+2-2x+2+3<0,解得x>7(4分)综上所述,不等式的解集为{x|x<-1或x>7…(5分)(Ⅱ)令g(x)=f(x)-1=|x+m1-2|x-11-1,问题转化为函数g(x)有1个零点3,x <若m> -1,则g(x)={3x+m-3,-m≤x≤1,x+m+1,x>1此时g(x)的最大值为g(1)=m,此时m=0满足题设;…(7分)3,x <若m<-1,则g(x)3x1,1≤x≤x+m+1此时g(x)的最大值为g(1)=-m-2,令-m-2=0,得m=-2,满足题设;(9分)若m=-1,则g(x)=-|x-11-1<0,故m=-1不合题意,舍去综上所述,m=-2或m=0.··,,,·,,,,··,,·,,··,,,·,,,·,·,,··,·,,,·,·,,·,,··,·,,,·,,,·,(10分)< p>

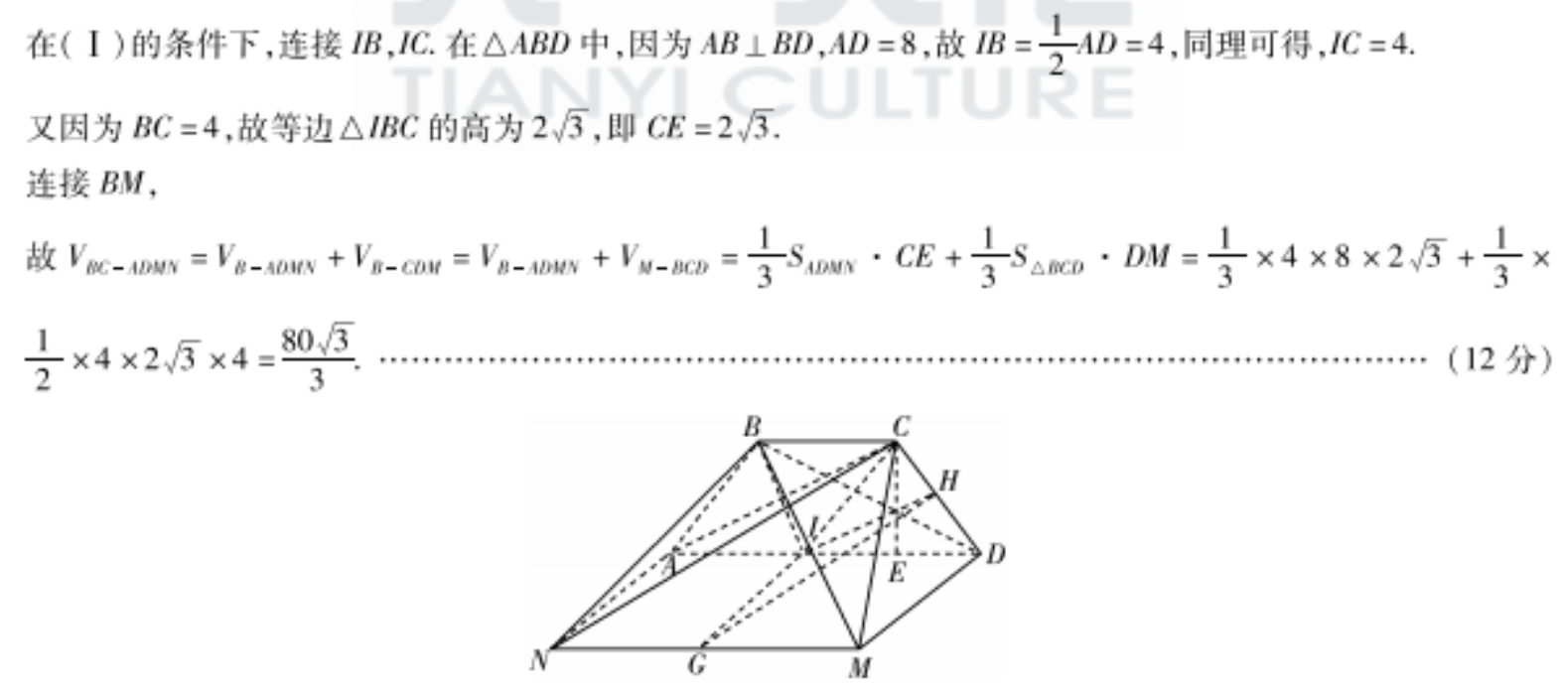
19.【命題意图】本题考查面面平行及多面体的体积,考查空间想象能力、推理能力与计算能力【解析】(1)当点/为线段AD的中点时,平面GH∥平面ACN(1分)下面给出证明:在矩形ADMN中,因为1,G分别是线段AD,MN的中点,故lG∥AN,又民G￠平面ACN,ANc平面ACN,故G∥平面ACN.………………………(2分)在△ACD中,因为,H分别为线段AD,CD的中点,故m∥AC又H￠平面ACN,ACC平面ACN,故H∥平面ACN(4分)因为G∩∥=l,HC平面GH,GC平面GH故平面GH∥平面ACN.……(6分)(Ⅱ)如图,过点C作CE⊥AD于E,因为线段MN在平面ABCD内的投影与线段AD重合,故平面ADMN⊥平面ABCD,而平面ADMN∩平面ABCD=AD,CEC平面ABCD,故CE⊥平面ADMN(8分)同理可得,DM⊥平面ABCD(9分)在(1)的条件下,连接BB,C.在△ABD中,因为AB⊥BD,AD=8,故B=-4D=4,同理可得,C=4ULTURE又因为BC=4,故等边△BC的高为23,即CE=23连接BM,E Vw-AMN=Ve-AouN +Vn-cow=VH-AwN +VM-acnwAveCF.S△mD·D3×4×8×234×23×4803(12分)D

以上就是2021-2022 英语周报母版外研第四期答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/14593.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。