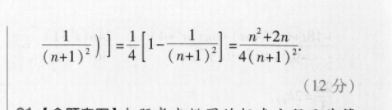
20.【命题意图】本题考查等差数列的定义、通项公式,利用裂项相消法求数列的前n项和,体现了逻辑推理、数学运算等核心素养(1)【证明】方法一由a,=2(b。+b1)(n≥2)及b=√S得an=2(√S+√S。1)(n≥2).(1分)由an=S-S1(n≥2)得S-S1=2(S+√S。)(n≥2),(2分)所以(√S。-√S。)(√S。+√S)=2(√S。+√Sn1)(n≥2)(3分)又√S。+√Sn1≠0,所以√S,-√S=2即b。-bn1=2(n≥2)又b1=√S1=√a1=2(5分)所以数列{b。}是首项为2,公差为2的等差数列(6分)方法二由an=S-S(n≥2)与b,=√S,得an=b2-b21(n≥2)(1分)又an=2(b,+bn1)(n≥2),所以b2-b21=2(b,+bn1)(n≥2),(2分)所以(b。+b。1)(b。-bn1)=2(b+b-1)(n≥2)(3分)因为Sn≠0,所以b。+bn1≠0所以b-b1=2(n≥2)(4分)又b1=√S1=√a1=2,(5分)所以数列{b。}是首项为2,公差为2的等差数列(6分)(2)【解】由(1)知,b。=2+2(n-1)=2n,所以S=4n2(7分)当n≥2时,an=Sn-Sn1=8n-4.(8分)当n=1时,a1=4也适合上式,所以an=8n-4.(9分)则anl8n+4S14n2·4(n+1)(10分)所以T。=4)+(2-n2+2n(n+1)(n+1)24(n+1)2(12分)

19.【命题意图】本题以北京冬奥会为背景,考查独立事件的概率和离散型随机变量的数学期望,体现了数学建模、数学运算、逻辑推理等核心素养【解】(1)设甲参加两个混合团体小项为事件A,则其概率为P(A)==(2分)故甲至少参加一个个人小项(即A的对立事件)的概率为P(A)=1-P(A)=1-≈3(4分)(2)由题意知,=2,3,4,6则P(=2)=cC=10×15(6分)P(E=3)=C:(CC+CC!)4x(5+12)3410×15=7(8分)P(=4)CC+C,Cc236+40CC10分)10×15故随机变量的数学期望E(5)=2×13万(12分)

以上就是2021-2022英语周报高考版第18期答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/13729.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。