2022-2023学生双语报第32期高一答案,目前学生双语报答案网已经整理了2022-2023学生双语报第32期高一答案的各科答案和试卷,更多学生双语报答案请关注本网站。

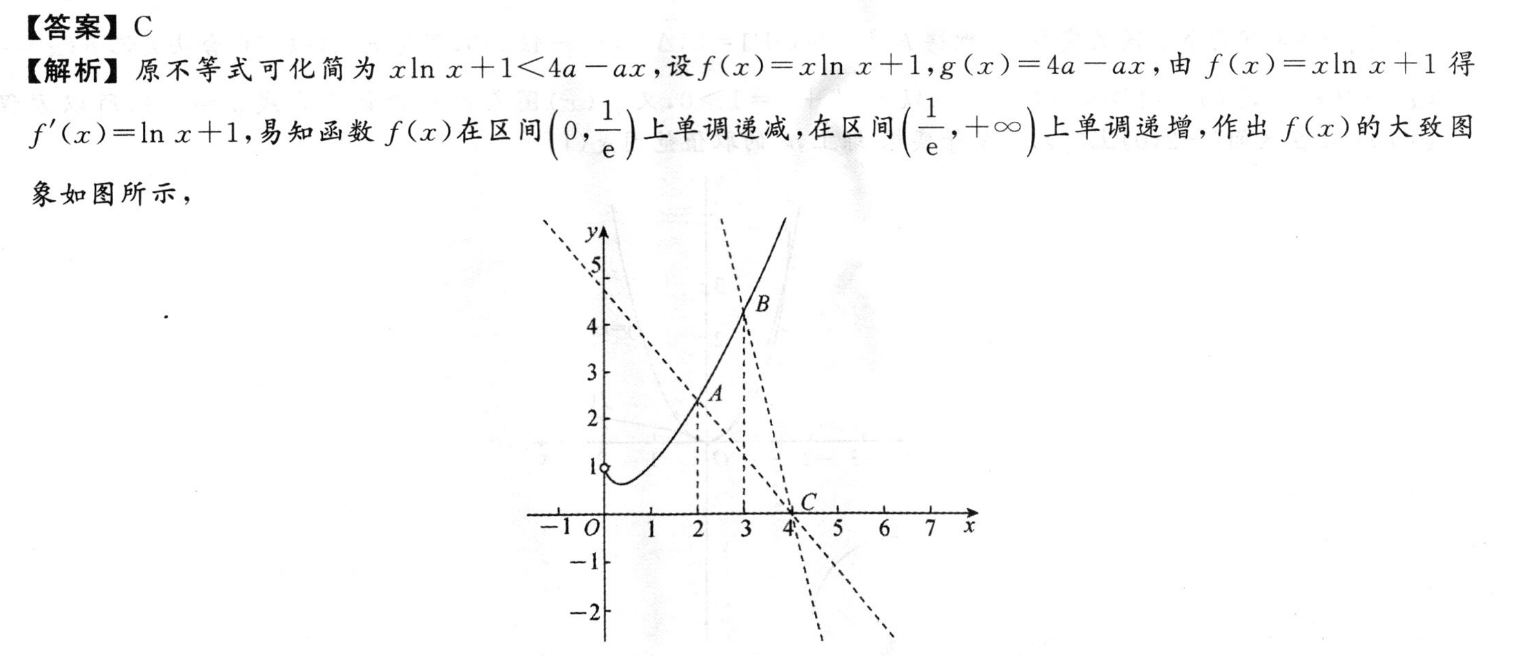

【答案】C【解析】原不等式可化简为xlnx+1<4a-ax,设f(x)=xlnx十1,g(x)=4a-ax,由f(x)=xlnx+1得了(x)=1nx十1,易知画数了(x)在区间0,日)上单调适减,在区同(日,十)上单调适增,作出了(x)的大致图象如图所示,B3、567文而函教g)=4a-ar恒过点C(4,0),要使关于x的不等式nx十a-a1<0有且只有两个整数解,则函数xg(x)的图象应介于直线AC与直线BC之间(可以为直线BC).又A(2,2ln2+1),B(3,3ln3+1),所以kAc=0-(2ln2十1D=-n2-2,kc=0-3in3+1D4-24-32=-3n3-1,所以-3n3-1≤-a<-1h2-号,所以1n2+2


解:(1)当a=0时,f(x)=xe,可得f'(x)=e(x十1).(1分)当x<-1时,f'(x)<0;当x>-1时,f'(x)>0.所以f(x)在区间(一∞,一1)上单调递减,在区间(一1,十∞)上单调递增.因为f-2)=-号,f2)-2e,f(-1)=-日,(2分)所以f(z)=-1,f()m=2e2.(3分)(2)由h(x)=f(x)-g(x)=(x-2)e+a(x-1)2,可得h'(x)=(x-1)(e十2a).①当a=0时,h(x)=(x一2)e,此时h(x)只有一个零点,故不成立.②当a>0时,h(x)在区间(一∞,1)上单调递减,在区间(1,+∞)上单调递增.因为h(1)=-e<0,h(2)=a>0,当a≥2时,h(0)=-2十a≥0;当

