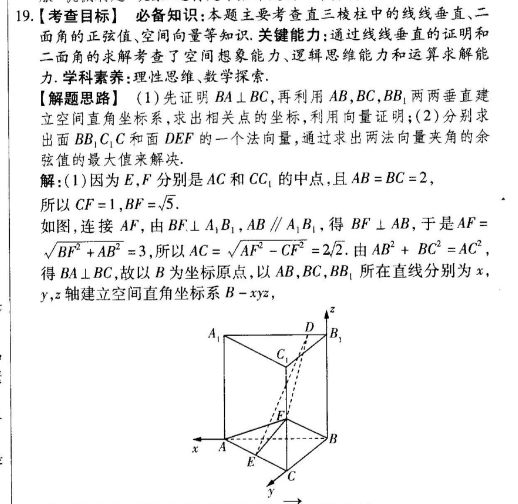
19.【考查目标】必备知识:本题主要考查直三棱柱中的线线垂直、二面角的正弦值、空间向量等知识.关键能力:通过线线垂直的证明和二面角的求解考查了空间想象能力、逻辑思维能力和运算求解能力学科素养:理性思维、数学探索【解题思路】(1)先证明BA⊥BC,再利用AB,BC,BB1两两垂直建立空间直角坐标系,求出相关点的坐标,利用向量证明;(2)分别求出面BB1C1C和面DEF的一个法向量,通过求出两法向量夹角的余弦值的最大值来解决解:(1)因为E,F分别是AC和C1的中点,且AB=BC=2所以CF=1,BF=√5.如图,连接AF,由BF⊥A1B1,AB∥AB,得BF⊥AB,于是AF=BF+ABF=3,所以AC=√AF-CF=2.由AB2+BC2=AC2,得BA⊥BC,故以B为坐标原点,以AB,BC,B1所在直线分别为x,y,z轴建立空间直角坐标系B-xy则B(0,0,0),E(1,1,0),F(0,2,1),BF=(0,2,1)设B1D=m(0≤m≤2),则D(m,0,2),于是DE=(1-m,1,-2)所以B.DE=0,所以BF⊥DE(2)易知面BB1C1C的一个法向量为n1=(1,0,0)设面DFE的法向量为n2=(x,y,2),n,又靂=(1-m,1,-2),E=(-1,1,1)所以(1-m)x+y-2z=0-x+y+z=0,令x=3,得y=m+1,z=2-m,于是,面DFE的一个法向量为n2=(3,m+1,2-m),所以cos(n1,n2〉=)2设面BCC与面DFE所成的二面角为6,则in6=√1-m(n1,m2),故当m=时,面BBCC与面DFE所成的二面角的正弦值最小为,即当B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小.【解題关键】本题求解关键是建立恰当的空间直角坐标系,确定相关点的坐标,再利用空间向量进行运算

【答案】8.C9.D10.A【解析】本文是说明文。文章介绍了一些魔术师表演的细节以及有关魔术的小技巧【8题详解】目的意图题。通过对文章主旨大意的理解以及文章最后两端讲述的魔术技巧,可知作者写这篇文章的主要目的是解释魔法的艺术。故选C项。【9题详解细节理解题。通过第二段 Magic shows are entertaining as long as the audience does not discover how the tricksare done..(只要观众不知道魔木是如何表演的,魔术表演就很有趣。以及“ The magician must keep peefrom noticing all the movements of his hands and from thinking about the secret parts of his equipment. (Exy/ip必须防止人们注意到他的手的所有动作和思考他的设备的秘密部分。)可知,对演出保密对于魔木的成功艮重要。故选D项【10题详解】推理判断题。通过倒数第二段“ For example the magician puts a small ball under one of several cups. The ballthen seems to jump from one cup to another or to change colour(例如,魔术师把求放在几个杯子中的下面。然后球似乎从一个杯子跳到另一个杯子或改变颜色)”以及最后一段 What actually happens is thatthe magician makes the cut or burned object disappear by quickly hiding it while the audience watches somethingelse.(实际发生的是,魔术师通过在观众观看其他东西时迅速隐藏它,使被切割或烧毁的物体消失)”可以推知,在文章最后两段中,作者举了两个例子。故选A项11题详解推理判断题。通过文章第一段“ The magician is a specially trained actor(魔术师是受过专门训练的演员)推知,表演魔术需要练习。故选C项

以上就是2018-2022 英语周报 高一 牛津 49答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/890.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。