8.参丐合柔解:选择①.(1)cos C+2cos Acos B=-Cos(A+ B)+2cos Acos B=cos Acos B+ sin Asin B=-cos(A-B)=24(2分)又A>B,且AB都为锐角,故sn(A-B)=2n(A-B)=24=1AmnB,所以tm2mnA=72(7+2-2又tan(A-B7tanA+2477(7tanA+24)(4分)又C <受,所以要 4,tanA>l,625所以,故

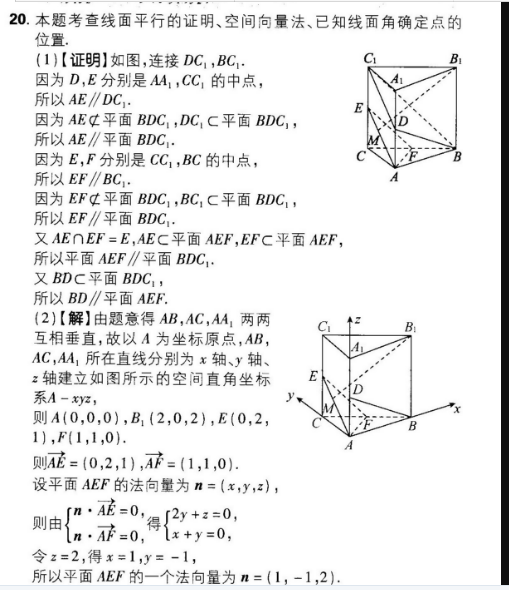
20.本题考查线面平行的证明、空间向量法、已知线面角确定点的位置1)【证明】如图,连接DC1,BC因为D,E分别是A1,CC1的中点所以AE∥DC因为AE￠平面BDC1,DC1C平面BDC,所以AE∥平面BDC因为E,F分别是CC1,BC的中点,所以EF∥BC因为EF￠平面BDC1,BC1C平面BDC1,所以EF∥平面BDC又AE∩EF=E,AEC平面AEF,EFC平面AEF,所以平面AEF∥平面BDC1又BDC平面BDC所以BD∥平面AEF2)【解】由题意得AB,AC,AA1两两互相垂直,故以A为坐标原点,AB,AC,A1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B1(2,0,2),E(0,21),F(1,1,0)则AE=(0,2,1),AF=(1,1,0)设平面AEF的法向量为n=(x,y,xz),+z=00,令z=2,得x=1,所以平面AEF的一个法向量为n=(1,-1,2则AE=(0,2,1),AF=(1,1,0)设平面AEF的法向量为n=(x,y,xz),n·AE=0则由得2y+z=0,n0x+y=0令z=2,得x=1所以平面AEF的一个法向量为n=(1,-1,2)设=A=(0,2A,A)(0≤A≤1),又AB=(2,0,2所以B1M=AM-AB1=(-2,2A,A-2)若直线B1M与平面AEF所成的角为60°,则in60°=1cos(n,B1B,MIInlIB, mil1×(-2)+(-1)×2A+2×(A-2(-2)2+(2A)2+(A-2)26√636×√5A2-4A+8√5A2-4A+8解得A=0或A=4,即当点M与点A重合或=4时,直线B1M与平面AEF所成的角为60°【归纳总结】一般求线面角有如下方法(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角中的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,利用sin=h斜线段长,进行求角,其中可利用等体积法解垂线段的长度h(3)建立空间直角坐标系,利用向量法求解,设a是直线的方向向量,n是平面的法向量,利用公式sin6=lcos(a,n》求解

以上就是2022第24期英语周报Unit 6课时练习答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/3956.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。