22证明:(1)由题意,得f(x)=- rcos z,x∈(0,2x)令f(x)=0,得x=2或x=2当x∈(0,2)时,(x)<0,f(x)单调递减;2·2)时,(x)>0,f(x)单调递增3当∈(22)时,(x)<0,()单调遥减,故x=是f(x)的极小值点,x=2是/(x)的极大值点综上.(x)在区间(0,2)内存在唯一的极大值点(5分)(2)因为g(x)=f()+csx=2-xsnx(一不x≤),所以g'(x)=-(sinx+ r cos .r).①当x∈|0,时,g(x)≤0,所以函数g(x)在区间上单调递减因为g(0)g()=3×3-x<0,所以函数g(x)在区间07上有唯一的零点.(7分)②当x∈「,x时,令h(x)=-(sinx+ xcos.),因为h(x)= rsin u-2cosx>0所以h(x)=g'(x)在区间上单调递增又g'(x)·g(7)=-x<0所以存在唯一∈(2),使,2=,(分所以当x∈「5,x)时,g(x)<0,当x∈(x,x)时g'(x)>0,所以g(x)在区间2’x。)上单调递减,在区间(x0,上单调递增.<0,g(r)>0,所以g(所以函数g(x)在区间「,x。)上没有零点,在区间[x,r)上有唯零点,所以函数g(x)在区间[0,丌]上恰有2个零点又g(x)为偶函数,且g(0)≠0,所以函数g(x)在区间-x,0)上也恰有2个零点综上,函数g(x)在区间[一x,x]上恰有4个零点(12分)

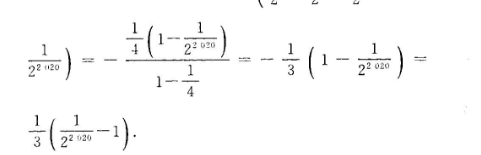
16.-11)【解析】因为Sn=(-1)"a当n=3时时,a1+a2汁+a:+a4a-1所以a1+a2+16②.由①②得“.=-16·当n≥2时,San=S,-Sn-1=(-1)"an+-1)+(2)当n为奇数时=()an-1;当n为偶数时故n为奇数,所以S,=2,n为奇数,n为偶数0,n为偶数所以S1+S2+…+S2020=一+(1-z2=)22043(22020

以上就是2022七年级外研英语周报第三十九期答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/17845.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。