21.【命题意图】本题考查导数在证明不等式及函数零点问题中的应用,考查推理能力与计算能力解析】(1)依题意(x)=hm2-2x,令g(x)=f(x)-2x+3=n+-4x+3,则g'(x)41分)故当x∈时,g(x)>0,当x∈(,+∞)时,g(x)<0(2分)故[g(x)]m=(4)41+3=2-ln8<0,即g(x)<0在(0,+∞)上恒成立,故f(x)<2x-3在(0,+∞)上恒成立(4分)(Ⅱ)依题意,mx-mx+m=0.设h(x)=ln2~m、4,则问题转化为函数h(x)有三个不同的零点4h'(x)(x>0)(5分)令k(x)=-mx2+x-4m,IANYI CULTURE当Δ=1-16m2≤0,即m≥一时,h'(x)≤0,h(x)单调递减,不可能有三个不同的零点;当4=1-16m20.即0 0,216m2>0,(6分)又k(x)=-mx2+x-4m的图象开口向下,所以当0 0,h'(x)>0,当x>x2时,k(x)<0,h'(x)<0.…(7分)因为h(2)=0,x1x2=4,故x1<2 ……(10分)24当0 (+)=-2×+1所以(m)在(0+)上单调递增所以hp(m) 0.>为(11分)所以由零点存在性定理可知,M(x)在(x2,)上有一个根,设为xo,又h(xn)+=0,得H()=0,故0<

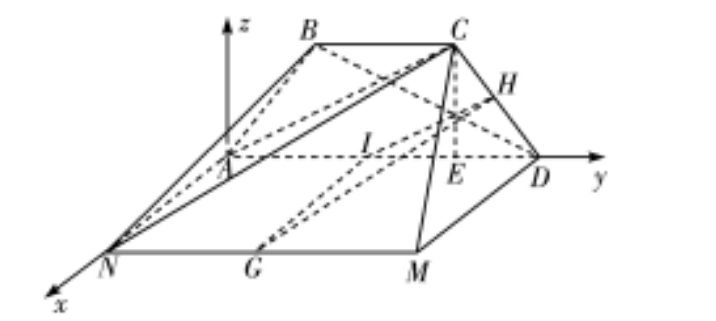
18.【命題意图】本题考查面面平行及线面角的正弦值,考查空间想象能力、推理能力与计算能力【解析】(1)当点/为线段AD的中点时,平面GH∥平面ACN(1分)下面给出证明:在矩形ADMN中,因为l,G分别是线段AD,MN的中点,故lG∥AN又G￠平面ACN,ANc平面ACN,故G∥平面ACN444(2分)在△ACD中,因为I,H分别为线段AD,CD的中点,故∥AC,又H￠平面ACN,ACC平面ACN,故∥平面ACN…(4分)因为G∩∥=1,Hc平面GH,Gc平面GH,故平面GH∥平面ACN(6分)(Ⅱ)如图,过点C作CE⊥AD于E,因为线段MN在平面ABCD内的投影与线段AD重合,故平面ADMN⊥平面ABCD,而平面ADMN∩平面ABCD=AD,CEC平面ABCD,故CE⊥平面ADMN.…,,(7分)以A为原点,AN所在直线为x轴,AD所在直线为y轴,过A作平行于直线CE的直线为z轴,建立如图所示的空间直角坐标系不妨设DM=2,由题可知,在Rt△ACD中,AE=3,DE=1,CE2=AE·DE=3,CE=3,则M(2,4,0),A(0,0,0),N(2,0,0),C(0,3,3)故心=(2,0,0),AC=(0,3,3)…(8分)0,t2x=0设n=(x,y,z)为平面ACN的法向量,则即LAC·n=0,3y+3z=0令y=1,则n=(0,1,-3)为平面ACN的一个法向量…(10分)而C=(2,1,-),故直线CM与平面ANC所成角的正弦值为CMn=2…(12分)I CHEM

以上就是2021-2022英语周报高三课标第四期答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/14438.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。