20.(12分)命题意图:本题考查导数的应用,零点存在性定理,利用导数研究函数的单调性,进而解决函数零点问题。第二问以学生熟悉的函数零点作为的设问方式,不至于完全阻学生于压轴题门外。第一问主要考查学生对具体函数的单调性与导函数符号内在联系的准确理解,指导学生养成严谨思考的数学思维习惯:第二问需要准确把握题意,在参数变化的情况下理清原函数图像与导函数图像的内在联系,可以结合草图分析,直观想象,进而得到破题方法,对学生综合能力要求高,需要一定的创新意识解析:(1)首先x∈(0,+∞),g(x)=f(x)=e2-x---(m+1),g(x)=e2+2-1由题意,g'(x)20在(O,+∞)上恒成立,即有e+-120,即x(e2-1)+m≥0,令G(x)=x2(e2-1)+m,x>0,易证G(x)在(0,+∞)上单调递增,所以G(x)>G(0)=m,所以m≥015分():由(1,m>0时,g()在(0+x)上单调递增,令g(x)=0得m=-x记F(x)=c-1x2-|1+e-x-1enx,则F(1)=01+F(e=eoe+ Ie(1-e)(√e+)<0,所以彐n∈(,e),使2F(x0)=0,令m,t(x)=e-x-1,则t(x)=e2-1,所以(x)在(1,e)上单调递增,所以t(x)>(1)=e-2>0,所以m>0,取m=m。,则g(x0)=0,f(x)=0,x∈(,x0)时,g(x)<0;x∈(x0,e)时,g(x)>0:所以f(x)在(1,x)递减,在(x0,e)递增,又f(x0)=0命题得证。…………………………………………………12分

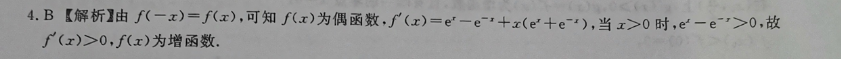
4.B【解析】由f(-x)=f(x),可知f(x)为偶函数,f(x)=e-e-+x(e+e-),当x>0时,e>0,故f(x)>0,f(x)为增函数

以上就是2021-2022年八年级新目标英语周报答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/13339.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。