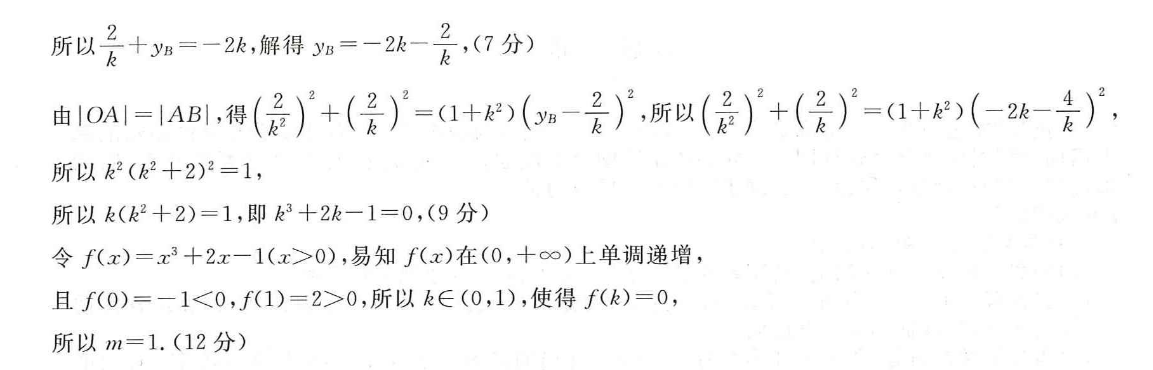
21.考的预测……解析几何解答题是新课标全国卷的必考内容,主要是考查直线与圆锥曲线的位置关系,载体主要是直线与椭圆,或者直线与抛物线,题目的综合性强,难度较大.预计2021年仍会以此形式考查解析几何解决问题的基本思想,考查考生分析问题、解决问题的能力以及良好的数学运算的基本素养思路……(1)先利用抛物线和圆的对称性,获得二者的一个交点,再代入抛物线求出其标准方程;(2)联立直线方程与抛物线方程得方程组,消去一个未知数得关于x或者y的二次方程,利用根与系数的关系及已知条件,求出待定系数k的方程,利用对应函数的单调性,可获得零点参考答案……(1)由对称性可知,MN两点关于x轴对称,所以点O到直线MN的距离d=√=(2)1,(2分)不妨设点M(1,2),代入y2=2px,得(2)2=2p,解得p=1,所以抛物线r的方程为y2=2x.(4分)(2)由题知直线OA的方程为y=k(k>0),与y=2x联立得A(是·是)所以直线AB的方程为y=是(x-是2)+2,即+2k2与y2=2x联立,得k2y2+2k2y-4-4k2=0,所以+yB=-2k,解得y=-2k2,(7分)k由OA|=14B,1(2)+(2)=(1+)(0-2),所以(是)+()=01+)(-2-k),所以k2(k2+2)2=1所以k(k2+2)=1,即k23+2k-1=0,(9分)令f(x)=x3+2x-1(x>0),易知f(x)在(0,+∞)上单调递增,且f(0)=-1<0,f(1)=2>0,所以k∈(0,1),使得f(k)=0,所以m=1.(12分)

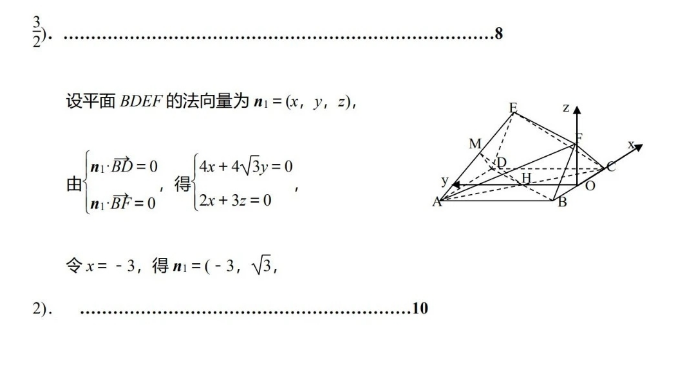
20.(本小题满分12分)(1)证明:如图,连接AC交BD于H,连接MHs、则MH为△ACE的中位线,所以M∥CE在平行四边形BDEF中,DBEFEF,CEC平面CEF, MH. DBC平面BDMEFnCE=E,MH∩DB=H∴平面CEF∥平面BDM(2)取BC的中点O,连接OF,OH,则OF⊥平面ABCD,OH⊥BC,以O为坐标原点,OC,OH,OF所在的直线分别为x,y,z轴建立空间直角坐标系则O0,0,0),A(-2,43,0),B(-2,0,0,C(2,0,0),D(2,4y3,0所以B=(4,43,0),BF=13,BO=2设OF=、BFBO3,则F0,0,3,B4,4,3M,4,3所以时(2,0,3),MF(-1,-43设平面BDEF的法向量为n1=(x,y,z)4x+4√3y=0由2x+3z=0令得n所以cs(m,M)=底少3√205205=-2054直线MF与平面BDEF所成的角的正弦值为3√20520512

以上就是英语周报中考复习版12期七年级。答案，更多英语周报答案请关注本网站。

本文地址： http://www.ncneedu.cn/post/10648.html

文章来源：admin

版权声明：除非特别标注，否则均为本站原创文章，转载时请以链接形式注明文章出处。